Trigonometry
The term Trigonometry can be described in the following points:
- Trigonometry is part of math that looks at how the lengths of the sides of a right triangle relate to the angles.
- Trigonometric ratios are used to figure out how this relationship works.
- These ratios are sine, cosine, tangent, cotangent, secant, and cosecant.
- The word “trigonometry” comes from Latin, and Hipparchus, a Greek mathematician, invented the idea.
What is Trigonometry
The word “trigonometry” is a Greek word. Its means “measurement of a triangle.” Therefore trigonometry is that branch of mathematics concerned with measuring the sides and angles of a plane triangle and investigating the various relations among them. Today the subject of trigonometry also includes another distinct branch that concerns itself with properties relations between and behavior of trigonometric functions. The importance of trigonometry will be immediately realized when its applications in solving the problem of mensuration, mechanics physics, surveying, and astronomy are encountered.
Trigonometry Definition
The branch of mathematics which deals with the study of triangles, their sides, and their angles are called Trigonometry. In short form, it is known as “trig.”
Trigonometry
Elements of Trigonometry
There are some important elements of trigonometry which are as follows;
- Angles
- Quadrants
Angles
An angle is the union of two non-collinear rays with standard endpoints.
OR
An angle is also defined as it measures the rotation of a line from one position to another about a fixed point on it.
In the figure, the first position OX is the initial line, and the second position, OP, is the terminal line or generating line of <XOP.

If the terminal side resolves in an anticlockwise direction, the angle described is positive, as shown in the figure.

If the terminal side resolves in a clockwise direction, the angle describes is negative, as shown in the figure

Quadrants
Two mutually perpendicular straight lines, XOX and YOY, divide the plane into four equal parts, each called a quadrant.
Quadrants

Thus XOY, X’OY, X’OY’, and XOY’ are called the 1st, 2nd, 3rd, and 4th quadrants, respectively.
- 1st Quadrant
In the first quadrant, the angle varies from 0° to 90° in an anti-clockwise direction and from – 270° to – 360° in a clockwise direction. - 2nd Quadrant
In the second quadrant, the angle varies from 90° to 180° in an anti-clockwise direction and – 180° to 270 ° in a clockwise direction. - 3rd Quadrant
In the third quadrant, the angle varies from 180° to 270° in an anti-clockwise direction and from – 90° to-180° in a clockwise direction. - 4th Quadrant
In the fourth quadrant, the angle varies from 270° to 360° in an anti-clockwise direction and from – 0° to-90° in a clockwise direction.
Types of Trigonometry
There are two types of Trigonometry;
- Plane Trigonometry
- Spherical Trigonometry
Plane Trigonometry
The Type of trigonometry which deals with the study of angles, triangles, and other figures in the two-dimensional plane is called Plane Trigonometry.
Plane Trigonometry

Spherical Trigonometry
Spherical Trigonometry concerns spherical triangles, which lie on a sphere, and the sides of which are circular arcs.
Spherical Trigonometry

Trigonometric Ratios
In trigonometry, six fundamental ratios help us to find the relationship between the lengths of the sides of a right triangle and the angle. Let’s look at how these ratios or functions work in the case of a triangle with a right angle. Think about a triangle with a right angle. The longest side is called the hypotenuse, and the sides next to and opposite the hypotenuse are called adjacent and opposite sides.

If the angle between the base and the hypotenuse of a triangle with a right angle θ, then;
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- tan θ = sin θ/cos θ
- Cot θ = Base/Perpendicular
- Cot θ = cos θ/sin θ
- Sec θ = Hypotenuse/Perpendicular
- Cosec θ = Hypotenuse/Perpendicular
| Functions | Abbreviation | Relationship to sides of a right triangle |
| Sine Function | sin | Opposite side/ Hypotenuse |
| Tangent Function | tan | Opposite side / Adjacent side |
| Cosine Function | cos | Adjacent side / Hypotenuse |
| Cosecant Function | cosec | Hypotenuse / Opposite side |
| Secant Function | sec | Hypotenuse / Adjacent side |
| Cotangent Function | cot | Adjacent side / Opposite side |
Trigonometric Reciprocal Functions
The reciprocal functions of Trigonometric Ratios are as follows;
| sin θ = 1/Cosec θ | Cosec θ = 1/sin θ |
| cos θ = 1/Sec θ | Sec θ = 1/cos θ |
| tan θ = 1/Cot θ | Cot θ = 1/tan θ |
Difference b/w Even and Odd Trigonometric Functions
The trigonometric function is either even or odd.
| Odd Trigonometric Functions | Even Trigonometric Functions |
| If f(-x) = -f(x) and the function is symmetric from the origin, it is called an odd function. | A trigonometric function is said to be even if f(-x) = f(x) and the position is the same on both sides of the y-axis. |
| Sin (-x) = – Sin x Tan (-x) = -Tan x Cosec (-x) = – Cosec x Cot (-x) = -Cot x | Cos (-x) = Cos x Sec (-x) = Sec x |
Trigonometric Ratios of Particular Angles
Trigonometric angles are the angles in a triangle with a right angle that can be used to show different trigonometric functions. The angles 0o, 30o, 45o, 60o, and 90o are often used in trigonometry. A trigonometric table shows the exact trigonometric values for each of these angles. 180o, 270o, and 360o are also important angles in trigonometry. In terms of trigonometric ratios, an angle in trigonometry can be written as,
- θ = sin-1 (Perpendicular/Hypotenuse)
- θ = cos-1 (Base/Hypotenuse)
- θ = tan-1 (Perpendicular/Base)
Trigonometric Ratio of 0o
Let the initial line revolve and trace a slight angle nearly equal to zero 0°. Take a point P on the final line.
Draw PM perpendicularly on OX.
PM = 0

Trigonometric Ratio of 30o or π/6
Let the initial line OX revolve and trace out an angle of 30°. Take a point P on the final line. Draw PQ perpendicular to P on OX. In a 30° right-angled triangle, the side opposite to the 30° angle is one-half the length of the hypotenuse, i.e., if PQ = 1 unit, then OP will be 2 units.

From fig. OPQ is a right-angled triangle
By the Pythagorean theorem, we have
(OP)² = (OQ)² + (PQ)²
(2)² = (0Q)² + (1)²
4= (0Q)² + 1
(0Q)² = 3
(0Q) = √3
Trigonometric Ratio of 45o or π/4
Let the initial line OX revolve and trace out an angle of 45°. Take a point P on the final line. Draw PQ perpendicular to P on OX. In a 45° right-angled triangle, the perpendicular length is equal to the length of the base, i.e., if PQ = 1 unit then OQ = 1 unit.

From figure by Pythagorean theorem.
(OP)² = (OQ)² + (PQ)²
(OP)² = (1)² + (1)² = 1+1=2
OP = √2
Trigonometric Ratio of 60o or π/3
Let the initial line OX revolve and trace out an angle of 60°. Take a point P on the final line. Draw PQ perpendicular to P on OX. In a 60° right angle triangle, the length of the Base is one-half of the Hypotenuse i.e., OQ = Base = 1 unit, then. OP Hyp. = 2 units
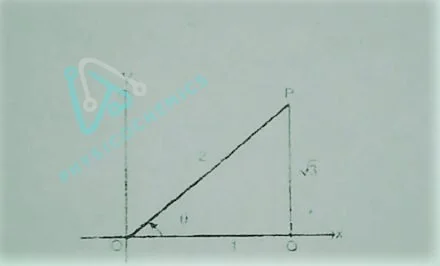
from a figure by Pythagorean Theorem:
(OP)² = (OQ)² + (PQ)²
(2)² = (1)² + (PQ)²
4 = 1 (PQ)²
(PQ)² = 3
PQ = √3
Trigonometric Ratio of 90o
Let the initial line revolve and trace out an angle nearly equal to 90°. Take a point P on the final line. Draw PQ perpendicular to P on OX.
OQ=0, OP = 1, PQ = 1 (Because they coincide y-axis).
Trigonometry Table
| Angles | 0° | 30° | 45° | 60° | 90° |
| Sin θ | 0 | ½ | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | ½ | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
Signs of Trigonometric Functions
The trigonometric ratios have different signs in different quadrants. We can remember the character of the trigonometric function by the “ACTS” or CAST rule. In “CAST,” C stands for cosine, A stands for All, S stands for Sine, and T stands for Tangent.

- First Quadrant
In the first quadrant, the sign of all the trigonometric functions is positive, i.e., Sin, cos, tan, Cot, Sec, and Cosec are all positive. - Second Quadrant
In the second quadrant, Sine and its inverse cosec are positive. The remaining four trigonometric functions, i.e., cos, tan, cot, sec, are all negative. - Third Quadrant
In the third quadrant, tan and its reciprocal cot are positive and the remaining four functions, i.e., Sin, cos, sec, and cosec, are all negative. - Fourth Quadrant
In the fourth quadrant, cos and its reciprocal sec are positive; the remaining four functions, i.e., Sin, tan, cot, and cosec, are negative.
Rectangular Co-ordinates and Sign Convention
In plane geometry, the position of a point can be fixed by measuring its perpendicular distance from each of two perpendicular called coordinate axes. The horizontal line (x-axis) is also called abscissa, and the vertical line(y-axis) is called ordinate.

The distance measured from point O in the direction OX and OY are regarded as positive, while in the direction of OX’ and OY’ are considered negative. Thus in the given figure OM1, OM4, MP1 and M₂P2 are positive, while OM2, OM3, M3P3 and M4P4 are negative. The terminal line, i.e., OP1, OP2, OP3, and OP4, are positive in all the quadrants.
Trigonometry Formulas
| Pythagorean Identities | Sum and Difference identities | If A, B, and C are angles and a, b, and c are the sides of a triangle, then, |
| 1- sin²θ + cos²θ = 1 2- tan2θ + 1 = sec2θ 3- cot2θ + 1 = cosec2θ 4- sin 2θ = 2 sin θ cos θ 5- cos 2θ = cos²θ – sin²θ 6- tan 2θ = 2 tan θ / (1 – tan²θ) 7- cot 2θ = (cot²θ – 1) / 2 cot θ | For angles u and v, we have the following relationships: sin(u + v) = sin(u)cos(v) + cos(u)sin(v) cos(u + v) = cos(u)cos(v) – sin(u)sin(v) sin(u – v) = sin(u)cos(v) – cos(u)sin(v) cos(u – v) = cos(u)cos(v) + sin(u)sin(v) The remaining formulas are given below | Sine Laws: a/sinA = b/sinB = c/sinC Cosine Laws: c2 = a2 + b2 – 2ab cos C a2 = b2 + c2 – 2bc cos A b2 = a2 + c2 – 2ac cos B |
Sum and Difference identities remaining formulas
What is Right Angle Trigonometry?
The branch of trigonometry known as right-angle trigonometry deals only with right triangles. A right triangle has a right angle, which is an angle with a measure of 90 degrees. In right-angle trigonometry, the ratios of a right triangle’s sides are used to calculate the angles and sides of the triangle.
right-angle trigonometry

In right-angle trigonometry, sine (sin), cosine (cos), and tangent (tan) are the three fundamental trigonometric ratios. They are defined as follows:
- Sine: In a right triangle, the ratio of the lengths of the sides directly opposite the angle and the hypotenuse is known as the sine of the arc. Sin is indicated by it (theta).
- Cosine: In a right triangle, the cosine of an angle is the ratio of the angle’s adjacent side’s length to the hypotenuse’s length. It has the symbol cos (theta).
- Tangent: In a right triangle, the angle’s tangent is the proportion of the lengths of its neighboring and opposing sides. It’s designated as tan (theta).
These ratios are employed in several trigonometric equations to determine the sides or unknown angles of a right triangle. Engineering, physics, and navigation are just a few disciplines that use right-angle trigonometry.
Application of Trigonometry
Trigonometry has been used in many fields, such as architecture, astronomy, surveying, etc. Some ways it can be used are:
- Oceanography, seismology, meteorology, the physical sciences, astronomy, acoustics, navigation, electronics, and many more.
- It can also be used to figure out how far away long rivers are, how tall a mountain is, etc.
- Trigonometry on a sphere has been used to find the positions of the sun, moon, and stars.
FAQ’s
Who is the father of trigonometry?
Trigonometry is a branch of math that looks at the relationships between the lengths of the sides of a triangle and the angles. Hipparchus is thought to have invented trigonometry. Hipparchus, a Greek mathematician from the second century BC, was the first to learn how to use trigonometry. He also made the first trigonometric table and solved many problems in spherical trigonometry.
What is the conclusion for trigonometry?
Its literal meaning is “triangle measurement,” but it is used for much more than just measuring triangles. Trigonometry may not be very useful in everyday life, but it does make it easier to work with triangles. It’s an excellent addition to geometry and accurate measurements, so it’s a good idea to learn the basics even if you don’t want to go further.
What is the golden formula of trigonometry?
Bisect BC at P; the right triangle ABP has angles 18° at A and 72° at P. We know that AB = τ and BP = 1/2; therefore
sin 18° = cos 72° = 1/(2τ) = (τ – 1)/2 .
From the Pythagorean theorem,
cos² 18° = 1 – sin² 18° = 1 – (τ – 1)²/4
= 1 – (2 – τ)/4
= (2 + τ)/4.
Therefore
cos 18° = sin 72° = (1/2)√(2 + τ).
cos 36° = sin 54° = τ/2 .
sin 36° = cos 54° = (1/2)√(3 – τ).
Why is tan called tan?
The term “tan” in trigonometry is short for tangent. The word tangent comes from the Latin “tangent”, which means “touching”. In trigonometry, the tangent function represents the ratio of the length of the opposite side to the length of the adjacent side of a right triangle, where the angle between the hypotenuse and the adjacent side is measured.
What is theta formula?
In math, the Greek letter theta (θ) is often used to represent an angle. Depending on the situation, theta can be used in many different formulas. These are a few examples:
The formulas for sine, cosine, and tangent:
sin(θ) = opposite/hypotenuse
cos(θ) = adjacent/hypotenuse
tan(θ) = opposite/adjacent
More Articles


